
先ずは図にするところからです.
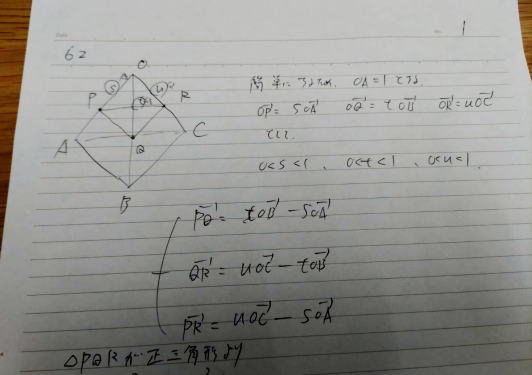
相似な図形は同じことが言えるので,
1辺1の長さにしました.

P,Q,Rという点はそれぞれOA,OB,OC上の点なので,1枚目ではs倍,t倍,u倍として表します.それからPQ,PR,QRの長さが等しいことから条件を2つ引き出します.
すると場合分けできました.
s=uまたはt=s+uです.
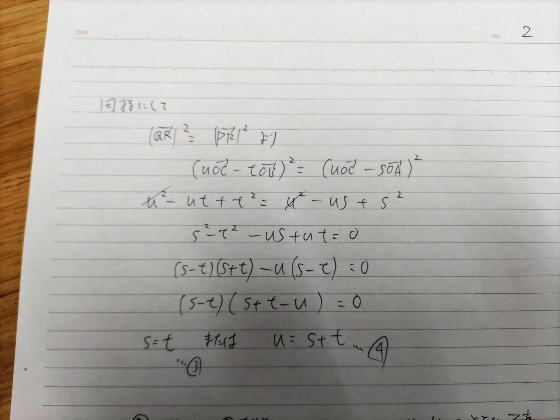
そこで,各ケースを検討してみます.

すると不適な条件の組合せが見つかってきました.
問題文を見ると,P,Q,Rは,正四面体の頂点にはならないので,s,t,uは0になることはないです.
これにより,s=t=uを言うことができ,三角形の相似が言えます.ラフ答案なので,書いてませんが,2組の辺の比とその間の角がそれぞれ等しいですね.中3最後のほうの内容です.分かる人は考えてみてくださいね.
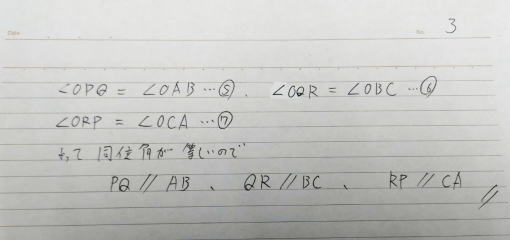
三角形の相似が言えたら,対応する角が等しいので同位角が等しいことが言えるので各辺の平行が言えて証明終わりですね.最後のちょんちょんも忘れずに.証明終わりのマークです.
