塾長ブログより ■９月１８日 　　休みなんですが，夕方からはいつも来てます．本当に必要な方はこういう時でも来るんですね．一応，塾部門としては開けてるんですよ．まだ誰も来ないので暇つぶしに東大の理系数学の過去問，解いてみました． ちょっとこれは面倒そうだからパスかｗ ２枚目は，数列も良さそうだし，一番下の第５問が取り組みやすそう． 取り組みやすいこの問題を解いてみます． 問題を書いてみると， ｍを２０１５以下の整数とする． ２０１５Ｃｍが偶数となる最小のｍを 求めよ． 組合せの記号を使った問題ですね． 先ずは，２０１５Ｃｎを用意してｎに１から順番にあてはめてみました．（ｍを使ってるのを忘れていたｗ） C４くらいで気付きました！C２の時，２０１４を２で割ると，奇数になり，偶数になりません．２０１２も４で割るとまだまだ奇数になって偶数が出てこない．そこでｎ番目ならどうかというのを調べてみます． 　　ｎを偶数として，２０１５からだんだん減っていった２０１５−（ｎ−１）がｎで割ると ２ｍという偶数になるとします． 式変形すると ２０１６＝ｎ（２ｍ＋１）となりました． ２０１６もどんな数か調べるため，素因数分解してみました． すると２５×６３＝２５×７×３２ となり，ここで２ｍ＋１は奇数なので ６３の約数が来ると思いました． ２ｍ＋１を６３の約数で１から順番に場合分けしてそれぞれのケースでｎを求めると ２ｍ＋１＝６３の時が一番ｎの値が小さいことが分かりました． 答えまで出ました！ 確かめもしてみます．ここで，問題のｍと自分の答案のｍが違っていたので，断り書きしないといけないことに気が付きました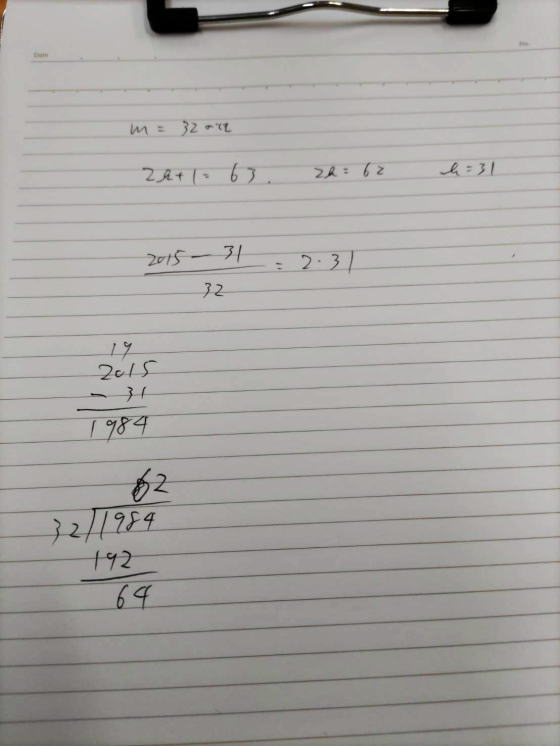． ラフ答案は，こんなところです． ここから言葉足らずな部分を補足していきます．（紺色のペンに替えました．） これで２０点全部頂きですｗ ひっ算の部分は，小学校４年から出来ますね．やってみてくださいね． ２０１６＝ｎ（２ｍ＋１）のところは，中２内容が使われており，素因数分解も中１で習うようになったのでいけるはずです． あとは，組合せですね．高１の場合の数と確率のところで習う項目です． 順列が５Ｐ３なら５から１つずつ数字を下げて３つかけるところを 組合せは順番気にしないので ３つの順列３Ｐ３で割るんですね． それが５Ｃ３のケースです． ８Ｃ４だとこんな感じです． ８Ｐ４ ８Ｃ４＝ ――――――― ４Ｐ４ ８・７・６・５ ８Ｃ４＝ ――――――― ４・３・２・１ ８・７・６・５＝８×７×６×５の意味です． 高校では，×の代わりに・を使います． エックスのｘとかけるの×を混同しないためですね． 所要時間：１５分程，初めて解きました． 普段は，頭が痛くなるので東大の問題は解かないですｗ このブログの編集のほうが，めっちゃ時間かかりました！もう７時なので２時間です．