運動量の保存３

テストを開始するには [テスト開始] ボタンを押してください。

問題

重心の運動

なめらかで水平な床上に質量mで長さが ℓ の一様な板ABが置かれている。この板上のA端に乗って静止していた質量2mの人がB端へと床に対して一定の速度vで歩く。図のように床面にx軸をとり、静止していた板のA端を原点とする。

　　　　　　　　

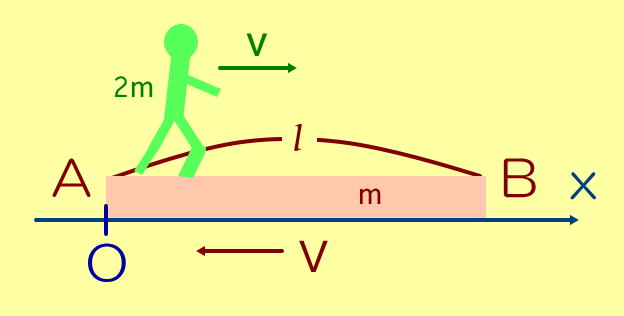
（１）人が板上を歩いている時、床に対する板の速度Vを求めよ。

運動量の保存により

0 = 2m・ - + 2 3 6 V v ℓ m + m・ - + 2 3 6 V v ℓ m

m - + 2 3 6 V v ℓ m = - + 2 3 6 V v ℓ m 2m - + 2 3 6 V v ℓ m 　V = - + 2 3 6 V v ℓ m - + 2 3 6 V v ℓ m - + 2 3 6 V v ℓ m

（２）　人がA端にいるとき、人と板とからなる物体系の重心の位置x_Gを求めよ。

　　　　　　　　

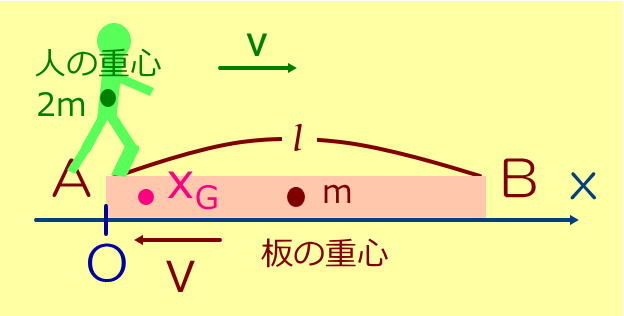
このときの板の重心は

	- + 2 3 6 V v ℓ m
x =	――	であるから
	- + 2 3 6 V v ℓ m

xG	=	2m × 0 + - + 2 3 6 V v ℓ m ・	- + 2 3 6 V v ℓ m ―― - + 2 3 6 V v ℓ m				=	- + 2 3 6 V v ℓ m - + 2 3 6 V v ℓ m ―――― - + 2 3 6 V v ℓ m	=	- + 2 3 6 V v ℓ m ―― - + 2 3 6 V v ℓ m
		―――――――――――――――――   - + 2 3 6 V v ℓ m - + 2 3 6 V v ℓ m + - + 2 3 6 V v ℓ m						―――――― - + 2 3 6 V v ℓ m - + 2 3 6 V v ℓ m

（３）　人がB端に着いたときの人の位置をx₁、板のA端の位置をx₂とする。このとき人と板からなる物体系の重心の位置x_G'をx₁とx₂を用いて表せ。

　　　　　　　　

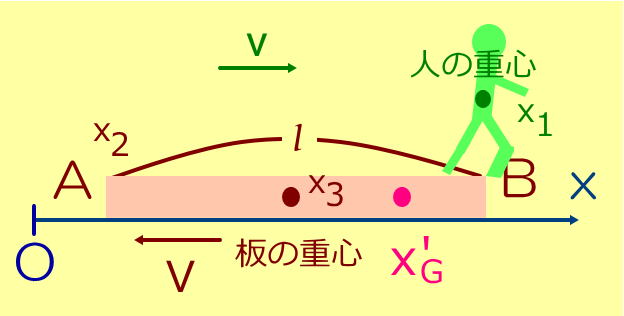
このときの板の重心の位置をx₃とすると、

x3

=

1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ + 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ ――――――――― 1 2 3 4 5 6 m x ℓ

より

xG'	=	1 2 3 4 5 6 m x ℓ	1 2 3 4 5 6 m x ℓ	・	1 2 3 4 5 6 m x ℓ	1 2 3 4 5 6 m x ℓ	+	1 2 3 4 5 6 m x ℓ	・	1 2 3 4 5 6 m x ℓ	1 2 3 4 5 6 m x ℓ
		―――――――――――――――――――――
		1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ + 1 2 3 4 5 6 m x ℓ

=	2m・x1 + m・	1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ + 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ ―――――――― 1 2 3 4 5 6 m x ℓ
	―――――――――――――――――― 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ + 1 2 3 4 5 6 m x ℓ

=	1 2 3 4 5 6 m x ℓ mx1 + mx1 + mx2 ―――――――――――
	1 2 3 4 5 6 m x ℓ ――――――――――――――― 3m

	1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ + 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ
=	―――――――――――――
	1 2 3 4 5 6 m x ℓ

（４）　x₁、x₂をそれぞれ ℓ を用いて表せ。

人と板からなる物体系には、水平方向に外力がかからないので、重心の位置は変わらない。したがってx_G = x_G'である。

　　　　　 1 2 3 4 5 6 m x ℓ 　　　　 1 2 3 4 5 6 m x ℓ x₁ + x₂
よって　―――― = ―――――――――
　　　　　 1 2 3 4 5 6 m x ℓ 　　　　　　 1 2 3 4 5 6 m x ℓ

1 2 3 4 5 6 m x ℓ x₁ + x₂ = 1 2 3 4 5 6 m x ℓ

また、板の長さは ℓ より、

x₁ - x₂ = 1 2 3 4 5 6 m x ℓ

連立方程式を解く。２つの式を足して

1 2 3 4 5 6 m x ℓ x₁ = 1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ

x1

=

1 2 3 4 5 6 m x ℓ ―― 1 2 3 4 5 6 m x ℓ

x2

=

1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ - 1 2 3 4 5 6 m x ℓ

= -

1 2 3 4 5 6 m x ℓ 1 2 3 4 5 6 m x ℓ ――――― 1 2 3 4 5 6 m x ℓ

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: