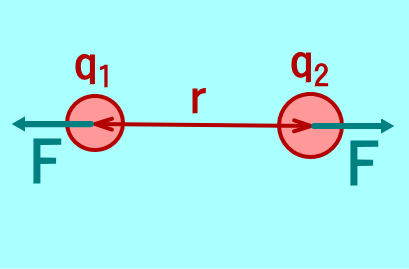
クーロンの法則・・・真空中で r (m) 離れた2つの点電荷 q1 (C) 、q2 (C) の間にはたらく静電気力 F (N) は
| |
|
――――――――
2 |
|
| F = k0 |
|
|
| |
|
|
| |
|
|
|
比例定数 k0 = × 10 N・m2/C2
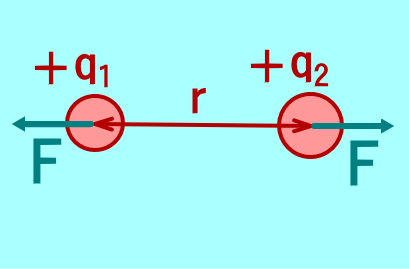
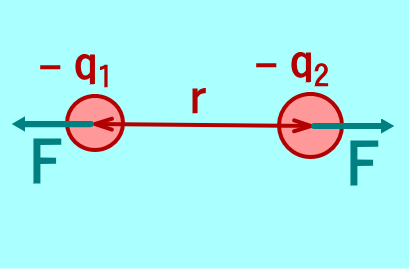
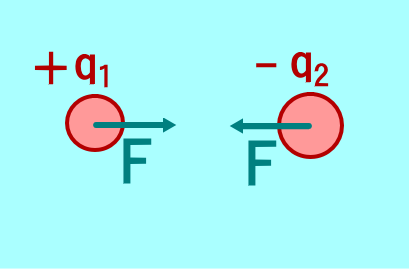
F が正のとき(せきりょく)、負のときとなる。
・・・体に帯電体を近づけると、帯電体に近い側には帯電体と種の電荷が、遠い側には種の電荷が現れる。
・・・体に帯電体を近づけると、原子内で電荷の偏りが生じ、隣の原子どうしで連鎖して電荷の偏りを伝える。結果として、導体ほどではないが、体の帯電体に近い側には帯電体と種の電荷が、遠い側には種の電荷が現れる。
電場(電界)・・・q (C) の電荷がF (N) の力を受ける電場の強さ E (N/C) は、
F =
により定義される。電場は、大きさ(強さ)と向きをもつである。
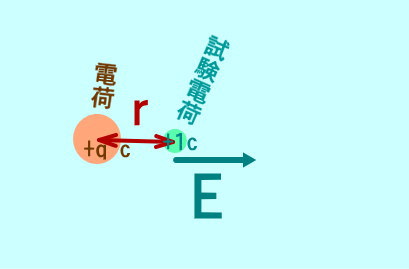
点電荷のまわりの電場・・・q (C) の点電荷から (m) 離れた点の電場の強さE (N/C) は、
| |
|
――――――
2 |
|
| E = k0 |
|
|
| |
|
|
| |
|
|
|
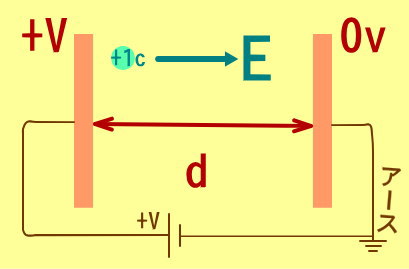
一様な電場内の電場・・・コンデンサーのd (m) 離れた2点間の電位差V (V)の一様な電場内において、電場の強さE (N/C)は、
| |
|
――――――
|
|
| E = |
|
|
| |
|
|
| |
|
|
|
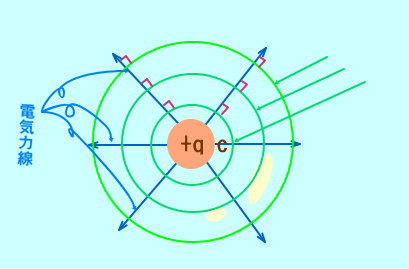
電気力線・・・正に荷電した点電荷が、電場中で静電気力を受けながら動く道すじを描いた線を電気力線といい、次のような特徴がある。
①電気力線は電荷から出て電荷に入る。
②電気力線が密なところほど、電場が。
③電気力線はわったりかれしたりしない。
④電場の強さが (N/C) のところでは、電気力線に垂直な面 1 m2 あたり 本の電気力線がある。
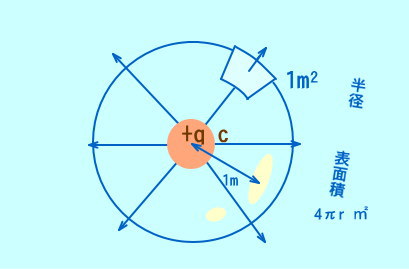
点電荷から出る電気力線の本数・・・点電荷のまわりの球面を考え、半径 1 (m) 、電荷を Q (C) とすると、電気力線の本数は、球の表面積×電場の強さ E = k0 Q だから
N =
電位と電位差
電位・・・+ 1Cの電荷を力にさからって動かす仕事をしたとき、電荷がもつ静電気力による位置エネルギーの大きさをという。
q (C) の電荷を、電位 0 の基準点から電位 V (V) の点まで運ぶ仕事 W (J) は、
W =
+ 1 C の電荷を、無限遠から正電荷の近くにある点まで動かすのに必要な仕事が 1 J であるとき、その点の電位は V (ボルト)であるという。この仕事は途中の道すじによって変わることはない。電位はベクトルではなく、である。
エネルギー・・・仕事で増えたエネルギーを U とすると、
U = W =
電位差・・・2点間の電位の差である。q (C) の点電荷を、電位V2 (V) の点からV1 (V) の点まで運ぶ仕事 W (J) が W = qV1 – qV2 = q(V1 – V2) で表されるとき、V1 – V2 (V) を(電圧)という。
点電荷による電位・・・q (C) の点電荷からr (m) 離れた点の電位 V (V)は、
| |
|
――――――
|
|
| V = k0 |
|
|
| |
|
|
| |
|
|
|
一様な電場内の電位・・・コンデンサーの強さがE (N/C) の一様な電場内において、電気力線に沿って d (m) 離れた2点間の電位差V (V) は、
V =
この式から、電場の強さの単位は (/) でもよいことがわかる。
| |
|
V (V)
――――――
d (m) |
|
|
|
|
| E (/) = |
|
|
= E (/) |
|
|
| |
|
|
|
|
|
| |
|
|
|
|
|
|
等電位面・・・電位の等しい点を結んだ面をという。等電位面に沿って電荷を動かす仕事は である。等電位面には次の特徴がある。
①電気力線と等電位面は互いにする。
②等電位面が密なところほど、電場が。
スマホ用解説動画へ
