ヤングの実験

テストを開始するには [テスト開始] ボタンを押してください。

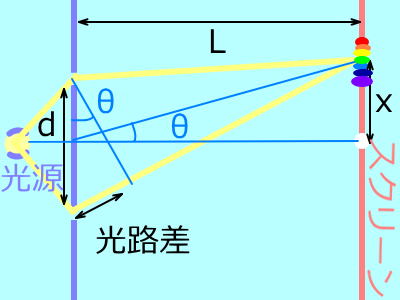
２つのスリットからの光路差は、

sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3

		sinθ cosθ tanθ d m x L λ 0 1 2 3 ―――――― sinθ cosθ tanθ d m x L λ 0 1 2 3
θが sinθ cosθ tanθ d m x L λ 0 1 2 3 に近いので、sinθ≒ sinθ cosθ tanθ d m x L λ 0 1 2 3 =

干渉縞の明線の間隔⊿xを求めるときは、

m = sinθ cosθ tanθ d m x L λ 0 1 2 3 を代入すると簡単に求められる。

d sinθ= sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3 のとき、明線が見られるので、

この式にm= sinθ cosθ tanθ d m x L λ 0 1 2 3 を代入。

		sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3 ―――――――――― sinθ cosθ tanθ d m x L λ 0 1 2 3
d sinθ=				= sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3

		sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3 ――――――――――― sinθ cosθ tanθ d m x L λ 0 1 2 3
⊿x = sinθ cosθ tanθ d m x L λ 0 1 2 3 =

理屈は、こうです。

		L(n+1)λ ――――――― d				Lnλ ―――― d				sinθ cosθ tanθ d m x L λ 0 1 2 3 sinθ cosθ tanθ d m x L λ 0 1 2 3 ―――――――――― sinθ cosθ tanθ d m x L λ 0 1 2 3
⊿x = xn+1 – xn =				–				=

⊿x = 3.0 × 10^-3 (m)、d = 4.0 × 10^-4 (m)、L = 2.0 (m)の場合、

波長λを求めると、

		d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ――――――――― d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青
λ=

		d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 × 10 d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 × 3.0 × 10-3 ――――――――――――――――――――――― d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青
λ=

λ= d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 × 10 ^{d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青} (m)


これは、可視光が d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 nm～ d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 nmの範囲に一致する。（n：ナノ= 10 ^{d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青} ）

光源に単色光を用いて、赤（650nm）、緑（550nm）、青（450nm）を用いると、⊿xは、 d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ＞ d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ＞ d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 の順に広がる。

装置全体を屈折率nの水中に入れると、⊿xは、dと d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 は変わらないが、 d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 が変化するので、変化後の明線の間隔⊿x’、波長をλ’とすると、

		d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ――――― d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青
λ’ =			λ

		Lλ’ ―――― d				L d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ――――― d d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青				d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ―――― d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青
⊿x ’=				=				=			⊿x

		d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ―――― d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青
よって			倍になる。

光源に白色光（ d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 の波長が入っている）を用いると、中央の明線は、 d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 色の明線ができるが、１次、２次、・・・の明線は、中央に近い側から d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 ～遠い側が d n L λ ⊿x 1 2.0 4.0 6.0 400 700 -4 -5 -6 -7 -8 -9 全て 白 赤 緑 紫 青 の連続スペクトルとなる。





スマホ用解答ページ

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: