電気容量とコンデンサー

テストを開始するには [テスト開始] ボタンを押してください。

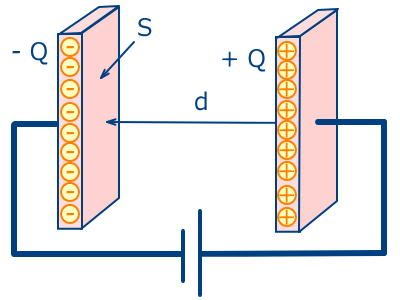
電荷： d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
極板の面積： d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 (m²)
極板間の距離： d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 (m)

問題では、必ず個々の値をMKSA単位系に直して解く。

1 mm = 10 ^{d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4} m

1 cm = 10 ^{d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4} m

1 cm² = 10 ^{d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4} m²　など

	1 ――――― 4πk0		d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 ――――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
Q =		・		・V

電気容量：C

	1 ――――――――――――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4		d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 ―――――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
C =		・		とおくと、

Q = d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4

単位は、 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 （ クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 ）


平行平板コンデンサーの電気容量Cは、
極板の面積Sに クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 し、
極板間の距離dに クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 する。


コンデンサーに蓄えることのできる電荷は非常に少量であるため、
電気容量の単位も次の単位がよく使われる。

1μF （ クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 ）= 10 ^{d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4} F

1p F（ クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 ） = 10 ^{d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4} F


誘電率：平行平板の間にセラミックなどの絶縁体をつめると、誘電分極により、平行平板にある電子と陽子がより クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 ようになる。この性質を考えるのに用いる値

	1 ――――――― 4πk0
真空の誘電率：ε0 =		= クーロン ファラド テスラ 比例 反比例 マイクロ ナノ ピコ 引き合う しりぞけ合う 6.67 8.31 8.85 9.0 × 10 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4

個々の誘電体の誘電率εと真空の誘電率ε0との比を比誘電率εrという。

	d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 ――――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
εr =

比誘電率は簡単に扱えるようになっている。（１倍よりは大きい値）

C = d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 C0

静電エネルギー：
コンデンサーが充電された状態で電荷が持つ位置エネルギー

	d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 ―――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
U =		d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 2

これを覚えておく。


あとは、Q = d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 を用いて変形して導く。

	d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 ―――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
U =		d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4

	d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 2 ――――――――― d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4 d ε0 ε εr k0 π C F Q S V -12 -11 -10 -6 -5 -4 -3 -2 1 2 4
U =

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: