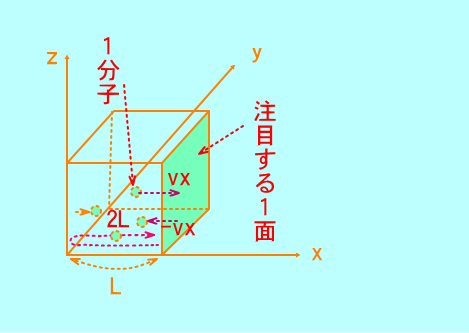
分子1個の質量をm とする.
1辺Lの立方体の1面(軸方向に衝突する面)に注目すると,
1回の衝突で壁への力積は
分子の運動量の変化より
2m=mvx - (-mvx)
時間t (s)では1面まで往復2Lの距離を速さvxで分子は移動するので
| t |
|
|
|
| ————— |
回,衝突する. |
|
|
| 2 |
|
|
|
力積の合計は,
|
t |
|
|
| 2m× |
————— |
=ft |
|
|
2 |
|
|
両辺,tで割ると
|
m2 |
|
|
| 力f= |
——————— |
|
|
|
|
|
|
立方体中の全分子N個による力は
|
mvx2 |
|
mvx2 |
|
|
|
| F=× |
————— |
= |
————————— |
|
|
|
|
L |
|
L |
|
|
|
x軸,y軸,z軸方向にランダムに分子は運動するので
v2=2+vy2+vz2=vx2
この式は3次元を3で割れる珍しい例である(笑)
vx2を中心とした式に変形すると,
|
2 |
|
|
|
| vx2= |
————— |
|
|
|
|
|
|
|
|
立方体の1面の面積はL2なので
|
F |
|
Nmvx2 |
|
Nmvx2 |
|
Nm2 |
|
| 圧力P= |
———— |
= |
————— |
= |
————— |
= |
———————— |
|
|
2 |
|
L3 |
|
|
|
V |
|
体積V=3(立方体の体積より)
