熱力学第1法則
⊿:内部エネルギーの変化量
気体の持つエネルギーを部エネルギーと呼ぶ.
気体の項目では,蒸気機関を想像するとよい.
石炭を燃やしてピストンを加熱する.
ピストンの中には,空気が入っていて
膨張することで運動に変わる.
加熱した熱量をJとする.
ピストンがした仕事がと表される.
この仕事を気体が部にした仕事という.
⊿U=-・・・熱力学第1法則
気体が外部にする仕事
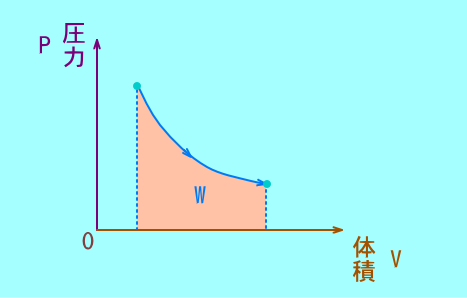
W=P⊿
PVグラフの積になる.
Tが一定の場合,
|
nRT |
(一定) |
|
| P= |
———— |
|
|
|
|
|
|
より反比例.
これを分するとWが求まる.
定積変化
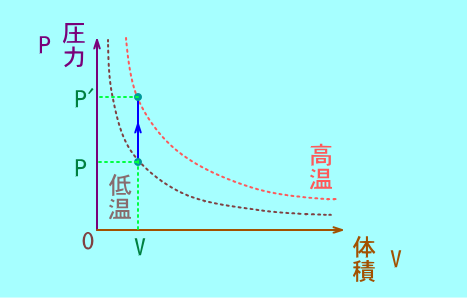
⊿U=,W=
PVグラフではに移動する.
定積モル比熱()
気体の体積が一定のとき(ピストンは動かない),
1モルの気体を1K温度上昇するのに必要な量
Q=nCv⊿T
|
|
|
|
| よりCv= |
———— |
R |
|
|
|
|
|
定圧変化
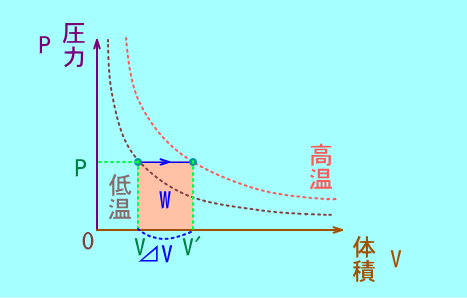
大気圧は,基本的に一定で1気圧より
ピストンが熱を加えてそのまま膨張した
状態を表す.
ピストン内部の気体の圧力は一定になる.
このとき,
W=⊿となり,
ピストンが膨張した分だけ仕事をする.
⊿U=QW=QP⊿V
ピストンが膨張すると
気体の温度Tは上がる.
定圧モル比熱()
ピストンがく状態で1モルの気体が
1K温度上昇するのに必要な量
P⊿V=nR⊿Tと状態方程式で表せるので
|
|
|
|
| Cp=Cv+= |
——— |
R |
|
|
|
|
|
マイヤーの関係
PVグラフでは,に移動する.
等温変化
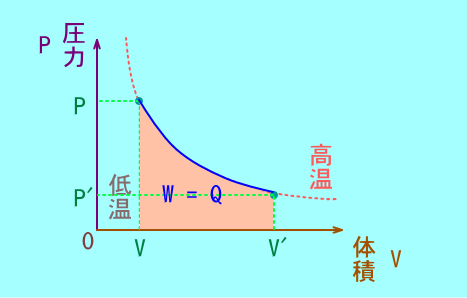
気体の温度を一定にして行うピストン運動
⊿U=
Q=
ピストンに加えた熱量がそのまま仕事に変わる.
この変化は,反比例のグラフになる.
|
nRT |
(一定) |
|
| P= |
———— |
|
|
|
|
|
|
比例定数nRTが大きいほど温度が高いので,
温度が低いときは,
グラフが縦軸と横軸にづく.
温度が高いときは,
グラフが上の内部(原点Oから遠いほう)に入っていく.
PVグラフでは,比例のグラフ上を移動する.
断熱変化
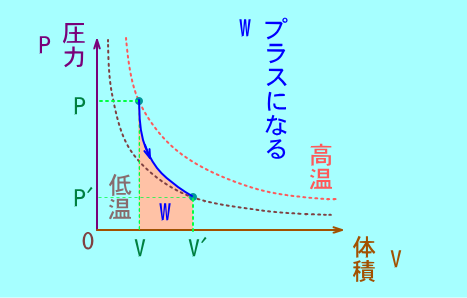
断熱膨張の図
ピストンをめない状態で起こるピストンの変化
Q=0
⊿U=W(このWは,気体が仕事された場合,マイナスとなる)
この変化は,ポアソンの法則
PVγ=一定が成立するようである.
|
Cp |
|
|
| γ= |
———— |
= |
———— |
|
Cv |
|
|
単原子分子の場合
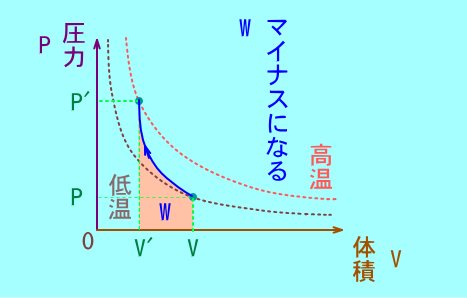
断熱圧縮の場合,発泡スチロールでおおわれた
ピストンを圧縮すると中の気体は温度ががるのを想像するとよい.
断熱膨張の場合は,ピストンを引っ張ると温度ががる.
PVグラフでは,体積が増えると温の反比例のグラフ上から
温の反比例のグラフ上に移動する.
気体の内部エネルギーは,
|
|
|
|
| U= |
——— |
nRT |
|
|
|
|
|
で表される.
問題によっては,
nRT=PVに置き換えることがよくある.
|
3 |
|
|
| U= |
—— |
|
|
|
2 |
|
|
