問題
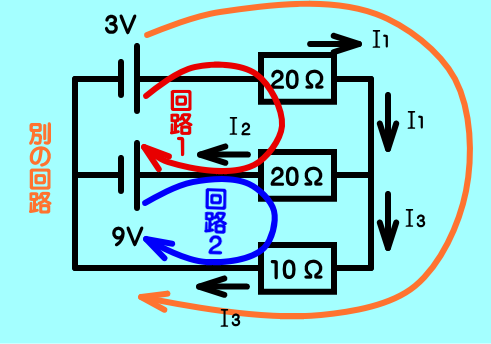
この回路を2つの部分に分けて考える.
電流の向きは自由に設定できる.実際には反対だった場合,の値として出てくる.
ここでは図のようにおいた.
回路2では,I2の向きは回路の向きと反対なのでをつける→③式
回路も自由に設定できる.全体を考えて別の回路のような取り方もできる.
図のような電子回路があり,電池が2つ,抵抗が3つ,つながれている.
キルヒホッフの第1法則により
流れ込む電流=出ていく電流の和
I1=+・・・① とおく.
キルヒホッフの第2法則により
起電力=電圧降下(抵抗×電流)の和および電池による電圧降下との和
回路1では,3=20+20I2+・・・② と表せる.
回路2では,9=-I2+10・・・③ と表せる.
3つの式から連立方程式を解く.
②より
20I1+20=3-9=-
10I1+10=-・・・②′
10I1=-10-
I1=--0.・・・②″
③より
10I3=20+
I3=2I2+0.・・・③′
②″と③′を①式に代入.
-I2-0.=I2+2I2+0.
-1.20=I2
I2=-0.
最初にI2の向きは仮においているが,反対の場合はこのようにマイナスで表される.
②″より I1=-(-0.)-0.30=
③′より I3=2×(-0.)+0.90=-0.+0.90
=0.
よって I1=(A)で,電流は流れない.
I2は向きが反対で時計回りで0.(A).
I3も0.(A)である.つまり回路2のみで電流が流れる.
お疲れ様でした。「採点」ボタンを押して採点してください。
