たてが4,よこが6の長方形ABCDがある.
点Pは点Aを出発してA→B,B→C,C→Dへと移動する.
点Pと点Aの間の道のりをxとし,⊿PADの面積をyとすると,
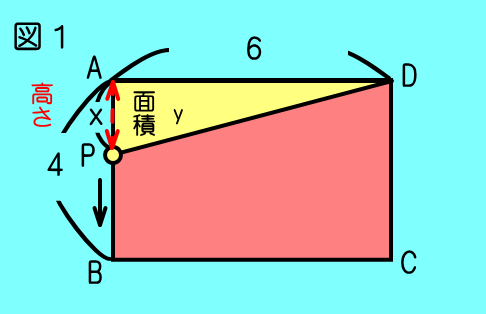
①A→B間では ≦x≦で底辺がAD,高さがAPより
|
1 |
|
|
| y= |
———— |
××= となる. |
|
|
|
|
|
|
|
|
|

②B→C間では ≦x≦+6=で図2から
底辺がAD,高さがABと同じ長さのだから
|
1 |
|
|
| y= |
———— |
××= となる. |
|
|
|
|
|
|
|
|
|
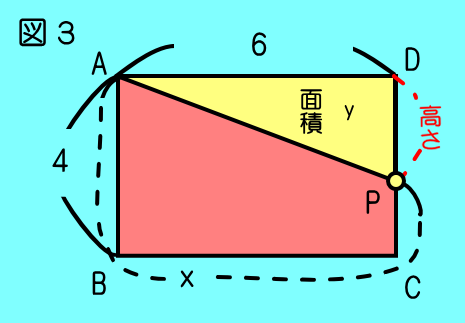
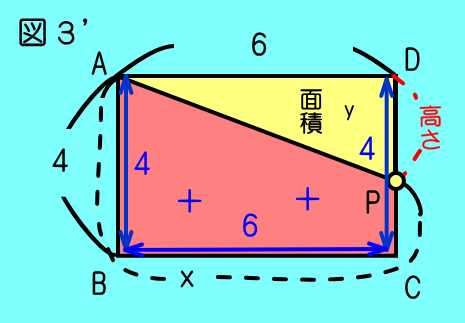
③C→D間では ≦x≦+4=で
底辺がAD,高さがDPとなり,
DP=AB+BC+CD-
=++-x
=-x と表せるので
|
1 |
|
| y= |
———— |
××(-) |
|
|
|
=(-)
=-x=-x+となる.
まとめると,
≦x≦で y=x
≦x≦で y=
≦x≦で y=-x+
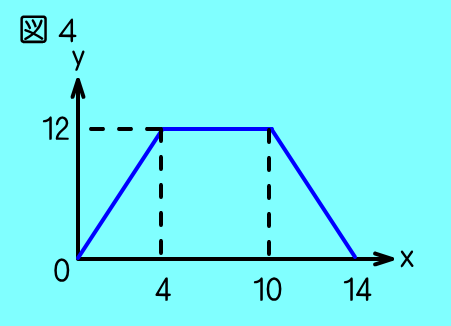
グラフはこのようになる.
