円周角の定理

図１．

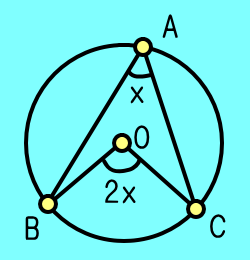
図１のように	BC	と円周上の点Aとの間で

なす角∠BACを 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 角という．

また	BC	と円の中心Oとの間で

なす角∠BOCを 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 角という．

∠BOC＝ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ ∠BACの関係がある．

中心角は 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 角の 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 倍である．




図２．

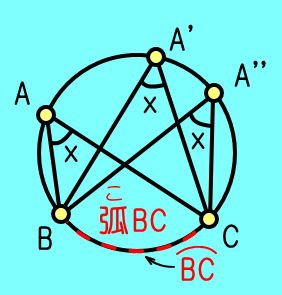
また図２のように	BC	と円周上の点A，A’，A’’となす角

∠BAC，∠BA'C，∠BA''Cはいずれも 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ ．

一般に同じ弧と円周上の点となす角は全て 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ ．




図３．


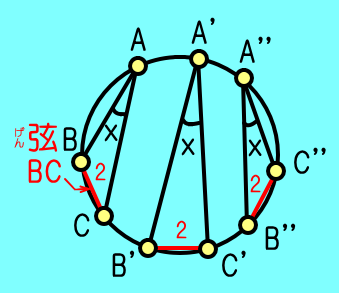
さらに図３のように弧の 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ が等しければ，円周角は全て 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ ．

∠BAC＝∠B'A'C'＝∠B''A''C''

ここでは 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ BC＝２，B'C'＝２，B''C''=２としているが，弧の長さも等しくなる．

しかし，弦が４でも弧の長さも 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 倍にはならないので気を付ける．あくまでも，弦の長さが 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ ときだけ，弧の 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ も等しいと考える．





図４．


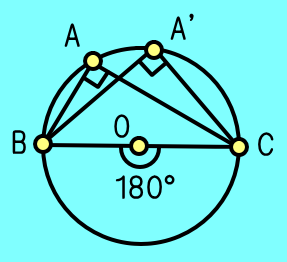
図４のように弧BCの弦BCが 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ の場合，中心角が
∠BOC＝ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ °より

その円周角∠BAC＝ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ °となる．

一般に 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ をなす円周上の２点から他の円周上の点を
結んだ円周角は全て 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ 等しい 異なる 角度 長さ 弧 弦 直径 半径 円心 円周 中央 中心 １ ２ ４ ８ ９ ０ °になる．

お疲れ様でした。「採点」ボタンを押して採点してください。