ある日をn日とすると,次の日は(n+),その次の日は(n+)日になる.
またn日の1週間後は(n+),(n+1)の1週間後は(n+),(n+2)の1週間後は(n+)日になる.
こういった知識を活かすとカレンダーの問題は簡単になる.

問題1.カレンダーの横1列の内,隣り合う3つの日にちの和は常に3の倍数になる.これを証明せよ.
解答.
これはある日をn日として(n+)日,(n+2)日を足すと
n+(n+)+(n+2)=3n+
=(n+1)となり,n+は自然数より3の倍数になる.//
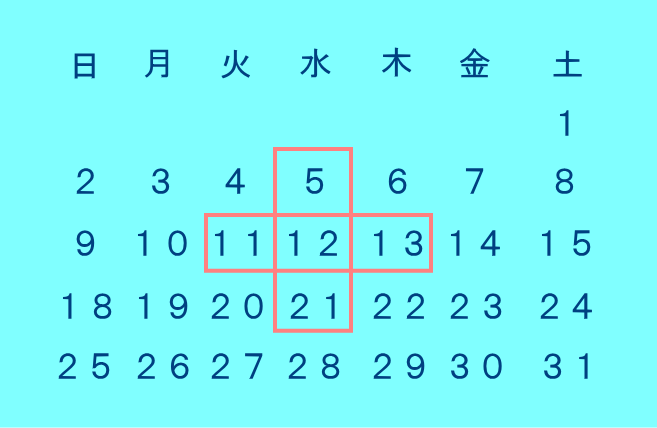
問題2.カレンダーのある日n日の縦の隣どうしと横の隣どうし4つの日にちとn日の和が5の倍数になることを証明せよ.
解答.
縦の隣の日は(n7)日と(n+)日.
横の隣の日は(n1)日と(n+)日.
これら5つの日を足すと
(n7)+(n+)+n+(n1)+(n+1)
=n
は自然数よりの倍数である.//

問題3.ある日n日の次の日とその次の日,1週間後,さらにその次の日,その次の日を足すと3の倍数になる.これを証明せよ.
解答.
n+(n+1)+(n+2)+(n+)+(n+8)+(n9)
=n+27=(2n+)
2n+は自然数より
3の倍数になる.//
お疲れ様でした。「採点」ボタンを押して採点してください。
