母平均と標本平均のずれの確率

テストを開始するには [テスト開始] ボタンを押してください。

問題 .

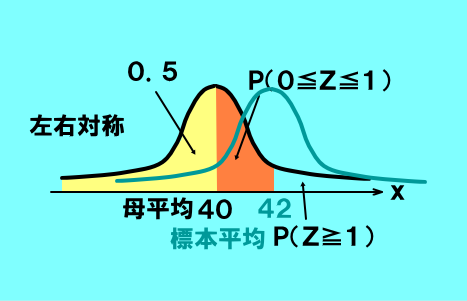
母平均ｍ＝４０，母標準偏差σ（シグマ）＝２０の大きな母集団（例えば，全国模試で５万人規模のケース）から，大きさ１００の無作為標本（受験生１００人）を抽出します．標本平均Ｘが４２以上になる確率を求めなさい．

標本平均Ｘに対して，

	Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ － Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８
Ｚ＝	————————	は大きさ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ が大きいとき，
	Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ (Ｘ)

標準正規分布Ｎ( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ， Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ )に近似的に従います．

Ｅ(Ｘ)＝ｍ＝ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８

	Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８
σ(Ｘ)＝	——————
		Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８

		Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８				２０
＝	――――――――				＝	———	＝ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８
						１０
		Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８

これよりＸは正規分布Ｎ( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ， Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ^２)に近似的に従います．

	Ｘ－ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８		１
Ｚ＝	——————————	＝	————	( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ － Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ )と置きます．
	Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８		２

Ｘ＝４２のとき

	１
Ｚ＝	————	( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ －４０)＝ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８
	２

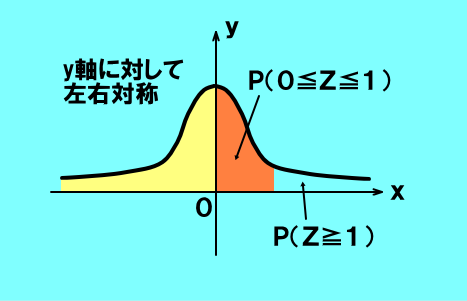
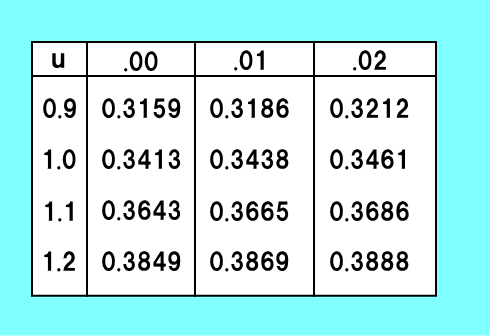
よってＸ≧４２である確率は，

Ｐ(Ｘ≧４２)＝Ｐ( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ≧ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ )

＝Ｐ( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ≧ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ )－Ｐ( Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ≦Ｚ≦ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ )

＝０. Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ －０. Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ＝０. Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ・・・答え

約 Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ Ｘ Ｚ ｍ ｎ σ ０ １ ２ ３ ４ ５ ６ ７ ８ ％であることを意味しています．
母平均よりも標本平均が２以上ずれる確率は結構あるということです．

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: