三角関数２

テストを開始するには [テスト開始] ボタンを押してください。

問題

次の問いに答えよ。

（１）

		3			3
sinθ	= -	―	、	π<θ<	―	π	のとき、
		5			2
cosθおよびtanθの値を求めよ。

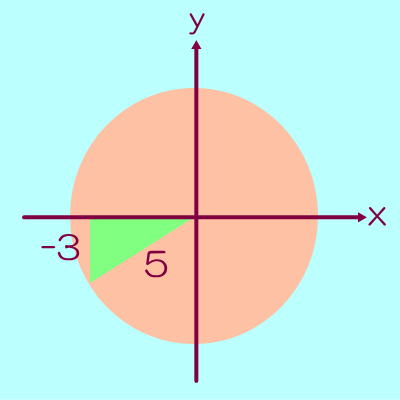
θの範囲から第３象限で、sinθの値から、

直角三角形の斜辺が √ + - 0 1 2 3 4 5 6 7 8 9 で、縦が √ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9 より下図のようになる。

横は、三平方の定理で(-3)² + (横)² = 5²、(横)² = 25 - 9 = √ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9

およびx座標はマイナスより √ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9


　　　　　　　　　　

	√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9
よってcosθ=	―――――	、tanθ=	―――――	=	―――
	√ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9

（２）　

	π
tanθ= -2、-	―	<θ<0のとき、
	2
sinθおよびcosθの値を求めよ。

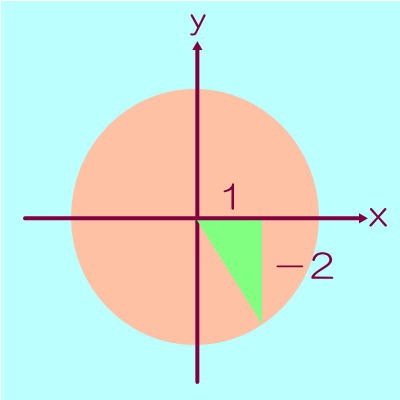
θの範囲から第４象限で、tanθの値より、

横が √ + - 0 1 2 3 4 5 6 7 8 9 で縦が √ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9

斜辺は三平方の定理より1² + (-2)² = √ + - 0 1 2 3 4 5 6 7 8 9 で、 √ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9


　　　　　　　　　　　

	√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9
よってsinθ=	―――――	、cosθ=	―――――
	√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9		√ + - 0 1 2 3 4 5 6 7 8 9 √ + - 0 1 2 3 4 5 6 7 8 9

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: