空間ベクトルを平面で考える

テストを開始するには [テスト開始] ボタンを押してください。

問題

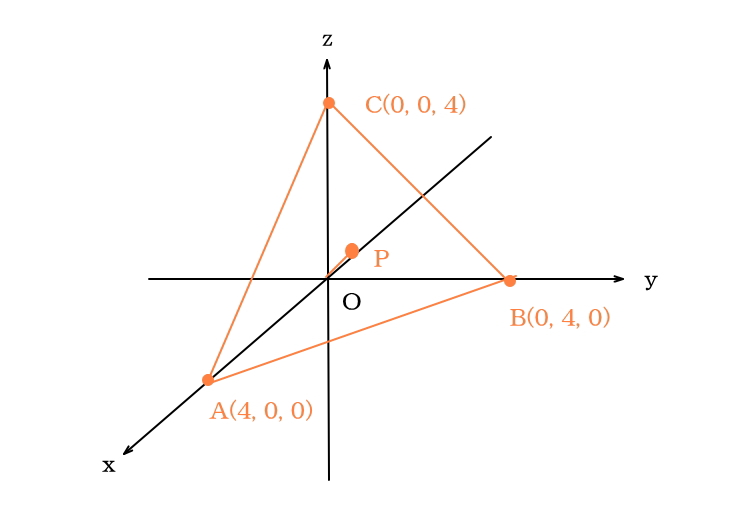
A(4, 0, 0)、B(0, 4, 0)、C(0, 0, 4)とする。原点Oから平面ABCに下ろした垂線の
足を点Pとする。点Pを求める。

APを	ABと	ACで表す。

AP = s	AB + t	ACと置く。

基本ベクトル１つめ

AB = ( 0 4 8 4s -4p -4s -4t , 0 4 8 4s -4p -4s -4t , 0 4 8 4s -4p -4s -4t ) - (4, 0, 0) = (-4, 4, 0)

基本ベクトル２つめ

AC = ( 0 4 8 4s -4p -4s -4t , 0 4 8 4s -4p -4s -4t , 0 4 8 4s -4p -4s -4t ) - (4, 0, 0) = (- 4, 0, 4)

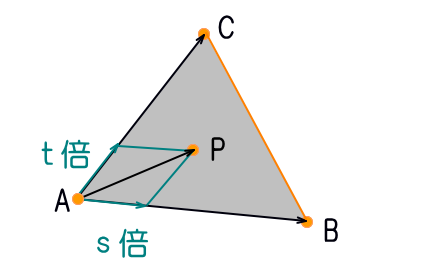
各成分にsとtをかけて

　　　　　　　↓sABベクトル　　　　　↓tACベクトル

AP = ( 0 +2 +4 4s -4s -4p -4t , 0 +2 +4 4s -4p -4s -4t , 0 +2 +4 4s -4p -4s -4t ) + (-4t, 0, 4t) = (-4s-4t, 4s, 4t)

APベクトルを用いてOPベクトルをつくる．

OP =	OA +	AP = ( 0 +2 +4 4s -4p -4s -4t 0 +2 +4 4s -4p -4s -4t 0 +2 +4 4s -4p -4s -4t , 4s, 4t)

　　　　　　　　　　　　↑文字文字数字の順番で



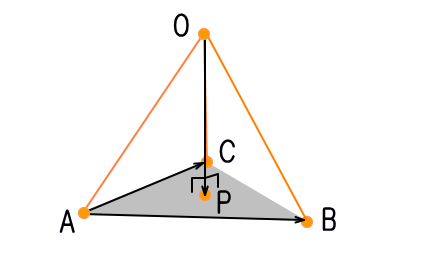
OPベクトルが平面ABCと垂直なので
平面上のどの直線もOPベクトルと垂直であることから

OPベクトルがABベクトルと垂直より

OP	・	AB = –4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 – 16 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 = 0

16で割って
–4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 – 1 = 0 …①

OPベクトルがACベクトルと垂直より

OP	・	AC = –4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 – 16 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 = 0

16で割って
–4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 – 1 = 0 …②

① より t = –4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2

ここから代入法でsを求める．
s + 2( –4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 ) – 1 = 0

s –4s -2s s 2s 3s 16s t 2t 16t 1 2 + –4s -2s s 2s 3s 16s t 2t 16t 1 2 – 1 = 0

–4s -2s s 2s 3s 16s t 2t 16t 1 2 = 1

	1 2 3 4 5 6 7 8 9 0						1 2 3 4 5 6 7 8 9 0
s =	――					t =	――
	1 2 3 4 5 6 7 8 9 0						1 2 3 4 5 6 7 8 9 0

	1 2 3 4 5 6 7 8 9 0		1 2 3 4 5 6 7 8 9 0		1 2 3 4 5 6 7 8 9 0	1 2 3 4 5 6 7 8 9 0
OP = (-	――	-	――	+ 4,	――	,――	)
	3		3		3	3

	1 2 3 4 5 6 7 8 9 0		1 2 3 4 5 6 7 8 9 0		1 2 3 4 5 6 7 8 9 0
= (	――	,	――	,	――	)
	3		3		3

ここまで出来ると，四面体OABCの高さも求まるので体積も求めることができる．

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: