軌跡つづき

問題

△OAPの重心を点Qとする．
点Qは，どんな図形を描くか．



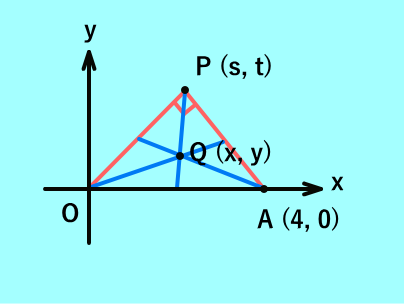
今度はP(s, t)とし，Q(x, y)とおく．

すると

( s t 0 1 2 3 4 5 6 7 8 9 – 2)² + s t 0 1 2 3 4 5 6 7 8 9 ² = 4　……①

が成り立つ．

Qは△OAPの重心より

	0 + s t 0 1 2 3 4 5 6 7 8 9 + s		s + s t 0 1 2 3 4 5 6 7 8 9
x =	―――――――	=	―――
	3		3

	0 + s t 0 1 2 3 4 5 6 7 8 9 + t		s t 0 1 2 3 4 5 6 7 8 9
y =	―――――――	=	―――
	3		3

s + s t 0 1 2 3 4 5 6 7 8 9 = s t 0 1 2 3 4 5 6 7 8 9 x, 　s = s t 0 1 2 3 4 5 6 7 8 9 x – s t 0 1 2 3 4 5 6 7 8 9 ……②

t = s t 0 1 2 3 4 5 6 7 8 9 y ……③


①，②，③より

( s t 0 1 2 3 4 5 6 7 8 9 x – s t 0 1 2 3 4 5 6 7 8 9 – 2)² + ( s t 0 1 2 3 4 5 6 7 8 9 y)² = 4

( s t 0 1 2 3 4 5 6 7 8 9 x – s t 0 1 2 3 4 5 6 7 8 9 )² + s t 0 1 2 3 4 5 6 7 8 9 y² = 4

(x – s t 0 1 2 3 4 5 6 7 8 9 )2 + y2 =	s t 0 1 2 3 4 5 6 7 8 9
	――
	s t 0 1 2 3 4 5 6 7 8 9

よって求める軌跡は，点( s t 0 1 2 3 4 5 6 7 8 9 , 0)を中心とし，

	s t 0 1 2 3 4 5 6 7 8 9
半径	――	の円周である．
	s t 0 1 2 3 4 5 6 7 8 9

ただし，△OAPが成立しないx軸上の点

	4		s t 0 1 2 3 4 5 6 7 8 9
(	――	, 0)，(	――	, 0)は除く．
	3		3

お疲れ様でした。「採点」ボタンを押して採点してください。