گ®ژ®پi‚¹‚¢‚µ‚«پjپF‚پ‚P‚ژپ{‚پ‚Q‚ژپ|‚Pپ{پEپEپEپ{‚پ‚ژ‚جچ\‘¢‚ً‚µ‚½ژ®پD
گ®ژ®‚o(‚ک)پپ(‚کپ|‚پ)‚p(‚ک)پ@‚ج‚ئ‚«پC
‚o()پپ(‚پپ|‚پ)‚p(‚پ)پپ‚OپE‚p(‚پ)پپ‚ئ‚ب‚éپD
‚±‚جگ«ژ؟‚©‚ç‚o(‚ک)‚ھژ‚ء‚ؤ‚¢‚éˆِگ”‚ً’²‚ׂ邱‚ئ‚ھ‚إ‚«‚éپD
‚±‚جڈêچ‡‚حپC(‚کپ|)‚ًˆِگ”‚ةژ‚ء‚ؤ‚¢‚邱‚ئ‚ھ‚ي‚©‚éپD
‚±‚جگ«ژ؟‚ًڈè—]‚ج’è—‚ئ‚¢‚¤پD
ˆê”ت‚ةپC‚o(‚پ)پپ‚ج‚ئ‚«پC
گ®ژ®‚o(‚ک)‚ح(‚کپ|)‚ًˆِگ”‚ةژ‚آپD
‚o(‚‚)پپ‚O‚ب‚ç‚خپC
گ®ژ®‚o(‚ک)‚ح(‚کپ|)‚ًˆِگ”‚ةژ‚آپD
‚ـ‚½پCگ®ژ®‚o(‚ک)‚ًگ®ژ®‚q(‚ک)‚إٹ„‚ء‚½‚ئ‚«پC—]‚è‚ح‚q(‚ک)‚و‚èژںگ”‚ھ‚آ‚¢گ®ژ®‚ئ‚ب‚éپD
‚q(‚ک)‚ھ‚Rژںژ®‚ب‚ç—]‚è‚حژںژ®
‚q(‚ک)‚ھ‚Qژںژ®‚ب‚ç—]‚è‚حژںژ®
‚q(‚ک)‚ھ‚Pژںژ®‚ب‚ç—]‚è‚حگ”
‚ئ‚ب‚éپD
‚o(‚ک)‚ً(‚کپ|‚Q)‚إٹ„‚ء‚½‚ئ‚«پC—]‚è‚ھ‚PپEپEپE‡@‚إ
(‚کپ{‚R)‚إٹ„‚ء‚½‚ئ‚«پC—]‚è‚ھ‚UپEپEپE‡A‚إ‚ ‚éپD
‚±‚ج‚ئ‚«پC‚o(‚ک)‚ً(‚کپ|‚Q) (‚کپ{‚R)‚إٹ„‚é‚ئ
—]‚è‚حٹ„‚éگ®ژ®(‚کپ|‚Q) (‚کپ{‚R)‚ھژںژ®‚إ‚ ‚èپC‚»‚ê‚و‚è‚P‚آ
ژںگ”‚ھ‚¢‚پ‚کپ{‚‚‚ئ’u‚¯‚éپD
‚o(‚ک)پپ(‚کپ|‚Q) (‚کپ{‚R) (‚ک)پ{‚کپ{‚ئ’u‚‚±‚ئ‚ھ‚إ‚«‚éپD
‚؟‚ب‚ف‚ة‚p(‚ک)‚حڈ¤‚ً”™‘R‚ئ’u‚¢‚½‚à‚ج‚إ‚ ‚èپC‚±‚±‚إ‚ح‚ا‚¤‚¢‚¤ژ®‚©‚ح–â‚ي‚ب‚¢پD
ڈًŒڈ‡@‚و‚è‚o()پپ‚إ‚ ‚èپC
‚o()پپ(پ|‚Q) (پ{‚R) ‚p()پ{‚پپEپ{‚‚
پپپE‚TپE‚p(‚Q)پ{‚پپ{‚‚
پپ‚پپ{‚‚پپپEپEپE‡B
“¯—l‚ةپCڈًŒڈ‡A‚و‚è‚o(پ|)پپ‚إ‚ ‚èپC
‚o(پ|)پپ(پ|پ|‚Q) (پ|پ{‚R) ‚p(پ|)پ{‚پپE(پ|)پ{‚‚
پپپ|‚TپEپE‚p(پ|‚R) پ|‚پپ{‚‚
پپپ|‚پپ{‚‚پپپEپEپE‡C
‡Bژ®پC‡Cژ®‚و‚è
|
|
|
|
|
|
|
|
|
‚Q‚پ |
پ{‚‚ |
پپ |
‚P |
|
| پ| |
 |
پ|‚R‚پ |
پ{‚‚ |
پپ |
‚U |
|
|
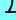 |
   |
  |
 |
   |
|
|
|
‚پ |
|
پپ |
پ| |
|
|
|
|
|
|
|
|
‚پپپپ|
‡Bژ®‚ة‚±‚ê‚ً‘م“ü‚µ‚ؤ
‚QپE(پ|)پ{‚‚پپ‚P
‚‚پپ‚Pپ{پپ
‚و‚ء‚ؤ—]‚è‚ح
‚کپ{
پپ‚کپ{‚ئ‚ب‚éپD
