平均値の定理

公式

平均値の定理




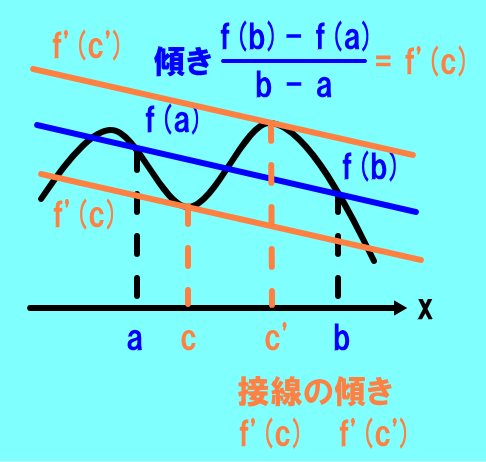
関数f(ｘ)が
ａ＜ｘ＜ｂで 連続 微分 ａ ｂ ｃ 可能で，

ａ≦ｘ≦ｂで 連続 微分 ａ ｂ ｃ のとき，

f( 連続 微分 ａ ｂ ｃ )－f(ａ)
——————————	＝f’( 連続 微分 ａ ｂ ｃ )
連続 微分 ａ ｂ ｃ －ａ

ａ＜ 連続 微分 ａ ｂ ｃ ＜ｂ
となる実数ｃが少なくとも一つ存在する．

問.

	ｅ３－ｅ	＜ｅ３
ｅ＜	—————
	２

が成り立つことを証明せよ．


ｅ＜ｘ＜ｅ^３でf(x)＝logｘは 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ 可能であり，

ｅ≦ｘ≦ｅ^３でf(x)＝logｘは 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ である．

	連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３
f’(x)＝	——————
	連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３

このとき，平均値の定理より

log 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ３－log 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３
		連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３
————————————————	＝	——————
連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ３－ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３		連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３

となるｃが存在する．（ｅ＜ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ＜ｅ^３）

logｅ^３＝ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ，logｅ＝ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３

逆数にすると

連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ３－ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３		連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ３－ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３
————————————	＝	————————————	＝ｃ
連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ － 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３		連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３

連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ＜ｃ＜ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ^３より

	ｅ３－ｅ
		＜ 連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ３
連続 微分 ａ ｂ ｃ ｘ ｅ １ ２ ３ ＜	——————————
	２

が成り立つ．


スマホ用解答

お疲れ様でした。「採点」ボタンを押して採点してください。