複素数平面
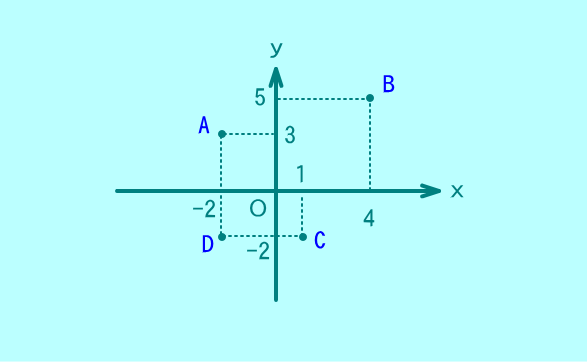
x:軸
y:軸
A:-+i
B:++i
C:12i
D:22i
共役複素数
z=+iとすると
__
z=abi
‗
z=abi
複素数の大きさ
|
|
|
|
| |z|2=z・ |
__ |
=2+b2 |
|
| z |
|
極形式
z=(θ+iθ)
r:大きさ
θ:実軸となす角度(時計まわり)
角という.
z1=r1(cosθ1+isinθ1)
z2=r2(cosθ2+isinθ2)のとき
z1z2=r1{cos(θ1θ2)+isin(θ1θ2)}
大きさr1
偏角θ1θ2
角度をアーギュメントargで表すときは
偏角はz1+z2と書く.
| z1 |
|
|
|
| ——— |
= |
—————— |
{cos(θ1θ2)+isin(θ1θ2)} |
| z2 |
|
r2 |
|
|
|
|
|
| 大きさ |
——— |
|
|
|
r2 |
|
|
偏角θ1θ2
角度をアーギュメントargで表すときは
偏角はargz1argz2と書く.
最近,二次試験にargが出ることがあるので
意味は上記のようであることを覚えておく.
