二次曲線ー放物線ー

テストを開始するには [テスト開始] ボタンを押してください。

問題 1.

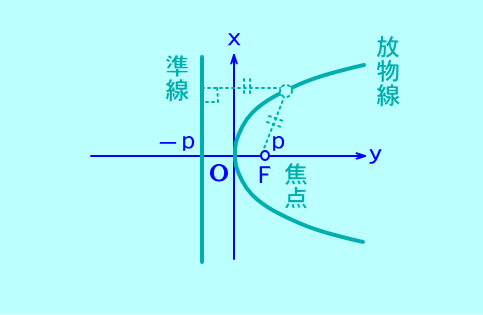
次の放物線の準線と焦点を求めよ。

（１）　y2 = 3x
公式は，ｐを使って
			y2 = p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 x
より，ｘの係数を比較して
			p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 = p + - 0 1 2 3 4 5 6 7 8 9
			p =	p + - 0 1 2 3 4 5 6 7 8 9 ―― p + - 0 1 2 3 4 5 6 7 8 9

よって焦点は、	(	p + - 0 1 2 3 4 5 6 7 8 9 ―― p + - 0 1 2 3 4 5 6 7 8 9	, 0)	、準線はx = -	p + - 0 1 2 3 4 5 6 7 8 9 ―― p + - 0 1 2 3 4 5 6 7 8 9

（２）　y = -	1 ―― 8	x2

両辺を－８×して

　　　x² = p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 y



公式は，ｐを使って

　　　x² = p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 y


ｘの係数を比較して

　　　 p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 = p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9


　　　p = p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9



よって今度はx² = 4pyのタイプだから

焦点はｙ軸上に来るので


焦点は(0, p + - 0 1 2 3 4 5 6 7 8 9 p + - 0 1 2 3 4 5 6 7 8 9 )、準線はy = p + - 0 1 2 3 4 5 6 7 8 9

問題 2.

焦点がF(	1 ―― 4	, 0)	、準線がx = -	1 ―― 4
である放物線の方程式を求めよ。

公式は
y2 = p x y + - 0 1 2 3 4 5 6 7 8 9 p x y + - 0 1 2 3 4 5 6 7 8 9 xで					p =	p x y + - 0 1 2 3 4 5 6 7 8 9 ―― p x y + - 0 1 2 3 4 5 6 7 8 9
だからy2 =	p x y + - 0 1 2 3 4 5 6 7 8 9 ・	p x y + - 0 1 2 3 4 5 6 7 8 9 ―― p x y + - 0 1 2 3 4 5 6 7 8 9			p x y + - 0 1 2 3 4 5 6 7 8 9

　　　y² = p x y + - 0 1 2 3 4 5 6 7 8 9

お疲れ様でした。「採点」ボタンを押して採点してください。

結果: