問題 1.
次の楕円の頂点と焦点を求めよ。
| |
|
|
|
x2
――
a2 |
+ |
y2
――
b2 |
= 1と照らし合わせて |
a = 、b = より
頂点は(, 0)、(, 0)、(0, )、(0, )
| 焦点はaとbを使って公式が、c = |
     
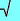 2 - 2 2 - 2 |
より |
| |
 |
      |
|
 |
   |
|
|
| c = |
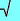 |
- |
= |
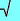 |
|
= |
|
焦点は、(, 0)、(, 0)
(2) x2 + 4y2 = 1
| これは、 |
x2
――
2 |
+ |
y2
―――― |
= 1より |
| ( |
――
|
)2 |
| |
|
|
|
|
| a = 、b = |
――
|
|
|
| |
|
|
|
| 頂点は(, 0)、(, 0)、(0, |
――
|
)、(0, |
――
|
) |
|
| |
|
|
|
|
|
| |
 |
     |
|
| 焦点は公式が、c = |
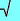 |
2 - 2 |
より |
| |
|
|
|
| |
|
   |
|
   |
|
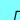      |
| c |
= |

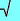 |
|
- |
――
|
= |
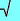
―――
   |
= |
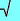
―――
|
|
| |
| |
|
|
|
|
|
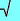 |
|
|
|
| |
|
|
|
|
|
| 焦点は、( |
  
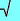
―――

|
, 0)、(- |
  
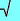
―――

|
, 0) |
|
| |
|
|
|
|
|
問題 2.
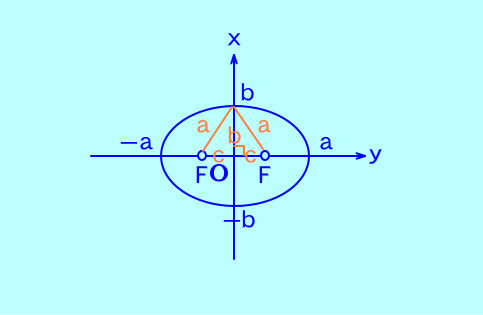
焦点が(2, 0)、(-2, 0)、焦点からの距離の和が8である
楕円の方程式を求めよ。
上の図で焦点から楕円上の点までの距離の和がa+a=
= =
bも上図の直角三角形の三平方の定理からa,cを使って
| |
 |
     |
|
|
|
| b = |
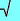 |
2 - 2 |
より |
|
|
| |
|
|
|
|
|
| |
 |
     |
|
 |
      |
| b = |
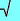 |
2 - 2 |
= |
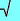 |
- |
| |
|
|
|
|
|
| |
 |
   |
|
|
 |
  |
| = |
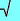 |
|
= |
|
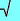 |
|
| |
|
|
|
|
|
|
よって楕円の方程式は
a2=42=16,b2=12より
x2
――――
|
+ |
y2
――――
|
= 1 |
お疲れ様でした。「採点」ボタンを押して採点してください。

2 - 2